저번 글에서 확률이 왜 중요한지 간단하게 생각해보았다. 그리고 확률에서 중요한 개념인 확률변수(Random variable)이란 어떤 것이고 확률변수가 정의되기 위해서 필요한 확률 공간에 대해서 알아보았다. 이번 글에서는 확률변수에 대한 추가적인 개념과 간단한 예를 통해서 확률변수에 대한 이해를 높이도록 하겠다.
1. 확률밀도함수(Probability density function, pdf)
확률밀도함수을 알기에 앞서 누적분포함수(Cumulative distribution function, cdf)에 대해서 알아보자. 확률밀도함수는 누적분포함수를 통해서 쉽게 유도할 수 있다. 누적분포함수(CDF)는 아래와 같이 정의된다.
$$ F_{X}(x) = P[{\zeta: X(\zeta) \le x}] = P_{X}[(-\infty,x]]$$
여기서 아래첨자 X는 확률변수이고 \( \zeta \)는 표본공간 내에서의 샘플을 말한다 (표본공간(Sample space)와 샘플(Sample)에 대해서 모른다면 이전 글을 참고하길 바란다. 즉, 누적분포함수란 이름에서 추측할 수 있듯이 표본에 대응되는 X라는 확률변수에서의 누적 확률이다. 더 자세히는 특정 샘플에 대응하여 확률변수가 가지는 x라는 값이하에서 발생되는 모든 샘플의 누적확률이다. 이 누적분포함수는 여러가지 특징을 가지는데 아래와 같다.
\( (i) \ F_{X}(\infty) = 1, F_{X}(-\infty) = 0 \)
\( (ii) \ x_{1} \le x_{2} \rightarrow F_{X}(x_{1}) \le F_{X}(x_{2}) \)
\( (iii) \ F_{X}(x) 는 \ 우연속 \ 함수이다. \ 즉, \ F_{X}(x) = \lim_{\epsilon \rightarrow 0}F_{X}(x + \epsilon) \)
(i)의 경우, 확률의 모든 누적합은 1이므로 명백하다. 또, 누적함수를 음의 무한대로 보낸 것은 아무것도 누적하지 않은 것이므로 0을 가진다.
(ii) 이것은 누적함수로서 당연히 가지는 특징이다. 누적분포함수가 x에 대해 증가함수임을 보여준다.
(iii) 아래 그림을 보자. 누적확률분포가 항상 연속적이다라고 생각하면 안된다. 누적확률분포는 오직 우연속 함수이다(. 좌측으로는 불연속할 수 있다.

본론으로 넘어와 확률밀도함수(Probability density function, pdf)에 대해서 알아보겠다. 확률밀도함수는 위에서 알아본 누적확률분표를 x에 대해 미분한 것이다.
$$ f_{X}(x) = \frac{dF_{X}(x)}{dx}$$
이 확률밀도함수는 오직 누적분포함수(\( F_{X}(x) \))가 연속함수일 때 정의된다. 위 그림과 같이 누적확률분포가 불연속일 때에는 확률질량함수(Probability mass function, pmf)라는 대체 함수가 존재한다. 그럼 확률밀도함수의 특징을 알아보자.
\( (i) \ f_{X}(x) \ge 0. \)
\( (ii) \ \int_{-\infty}^{\infty} f_{X}(\zeta)d\zeta = F_{X}(\infty) - F_{X}(-\infty) = 1. \)
\( (iii) \ F_{X}(x) = \int_{-\infty}^{x} f_{X}(\zeta)d\zeta = P[X \le x]. \)
\( (iv) \ F_{X}(x_{2})-F_{X}(x_{1}) = \int_{-\infty}^{x_{2}} f_{X}(\zeta)d\zeta - \int_{-\infty}^{x_{1}} f_{X}(\zeta)d\zeta = \int_{x_{1}}^{x_{2}} f_{X}(\zeta)d\zeta = P[x_{1} < X \le x_{2}]. \)
위 특징은 일반 도함수의 성질과 크게 다르지 않으므로 자세한 설명은 생략하도록 하겠다.
※ 설명의 편의를 위해서 누적분포함수, 확률밀도함수, 확률질량함수를 cdf, pdf, pmf라고 쓰도록 하겠다. 그리고 이 용어에 익숙해지는 편이 더 좋으리라 생각한다.
2. 흔한 확률밀도함수
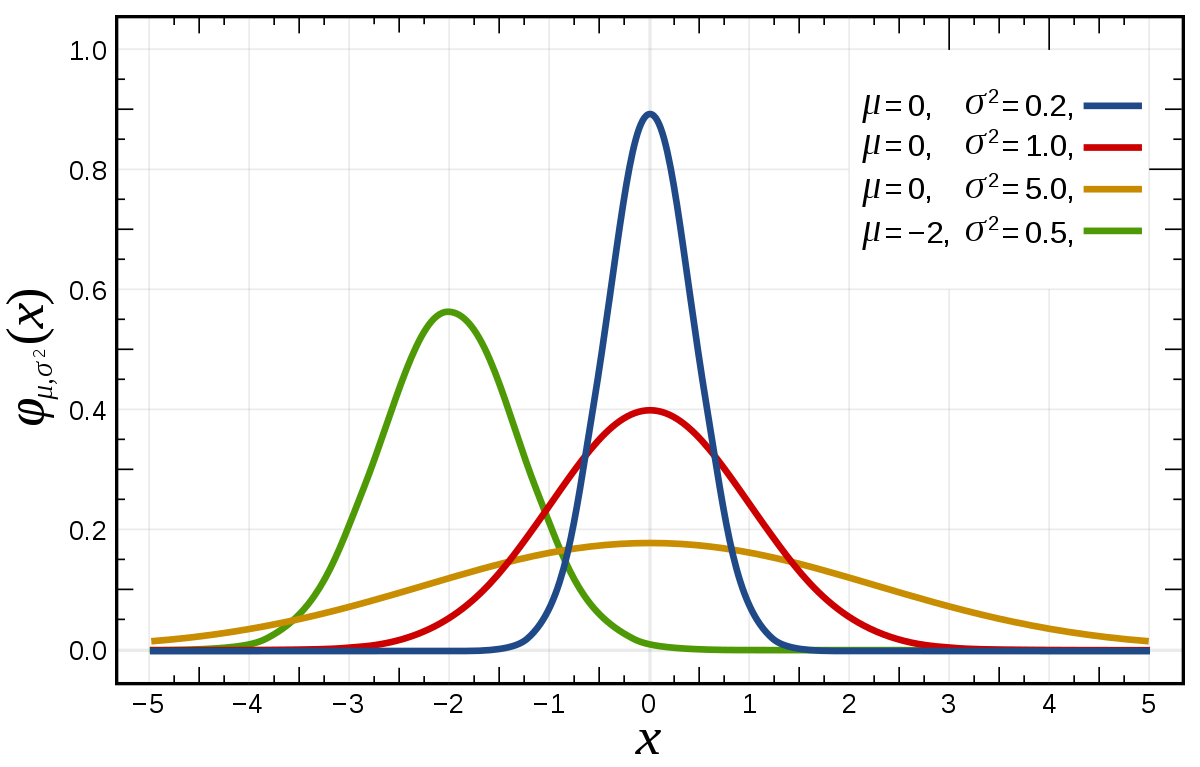
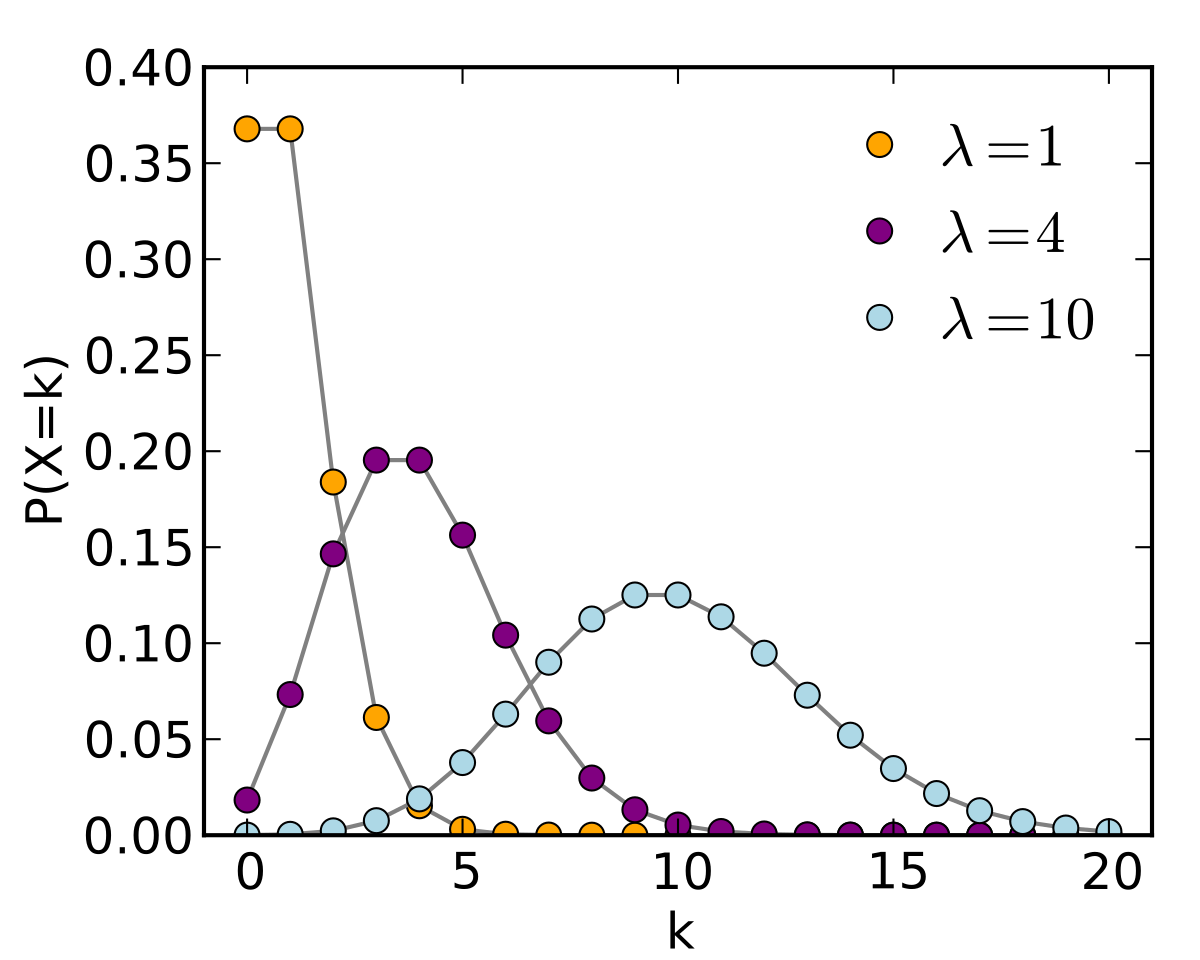

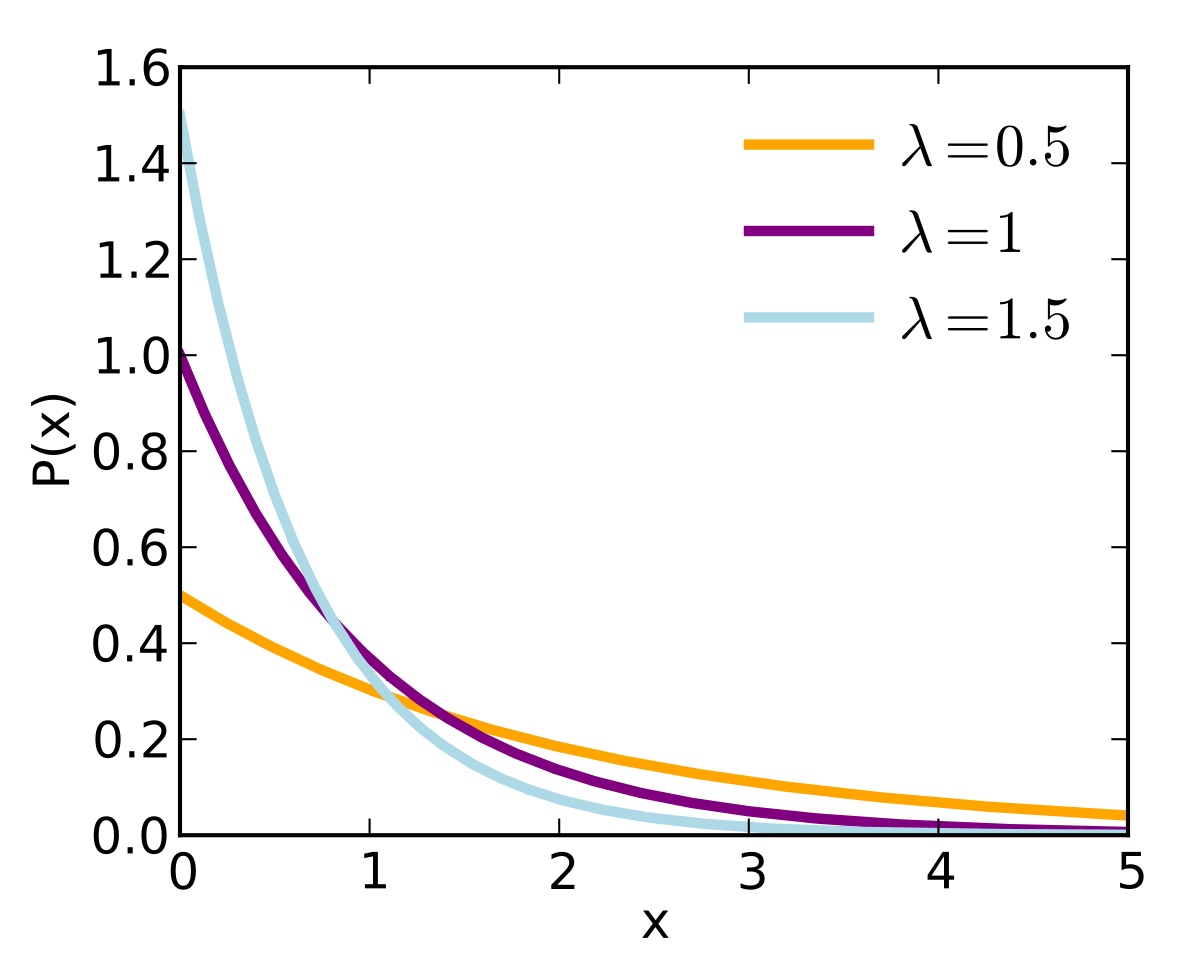
흔한 pdf란 공학자라면 한번쯤은 들어본 pdf를 말한다. 가우시안(Gaussian), 포아송(Poisson), 지수(exponential) 등이 있다. 본인에 분야에서 자주 쓰이는 pdf에 대해서는 알아두면 유용하게 쓰일 것이다. 본 글에서는 가우시안 확률분포에 pdf를 통해서 cdf를 유도해보도록 하겠다.
우리가 익히 알고있는 가우시안 함수의 형태는 pdf이다.
$$ f_{X}(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{1}{2}[\frac{x-\mu}{\sigma}]^2}$$
cdf는 pdf를 \( -\infty \)에서 x까지 적분한 결과이다. 그러므로 아래와 같이 쓸 수 있다. 그리고 가우시안 함수의 정규화 과정을 통해서 간단하게 치환할 수 있다.
$$ F_{X}(x) = \int_{-\infty}^{x} \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{1}{2}[\frac{x'-\mu}{\sigma}]^2} dx = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\frac{x-\mu}{\sigma}} e^{-\frac{1}{2}x'^2} dx $$
본 지수적분 형태는 더 이상 간소화하기 어려우므로 일반적으로 아래와 같이 간략히 표현한다.
$$ erf(x) = \frac{1}{\sqrt{2\pi}} \int_{0}^{x} e^{-\frac{1}{2} x'^2} dx $$
그래서 cdf는, 만약 \( x < 0 \) 이면, \( F_{X}(x) = \frac{1}{2} - erf(x) \) 이고
만약 \( x \le 0 \) 이면, \( F_{X}(x) = \frac{1}{2} + erf(x) \) 이다.
아래 그림은 다른 연속적인 분포를 가지는 pdf에 대해서 정리한 것이다. 잘 보이지 않는다면 클릭해서 확대해서 보는 것을 추천한다.

위 그림에 포아송 분포는 없다. 그 이유는 포아송 분포는 불연속함수이기 때문에 pdf를 가지지 않고 pmf를 가진다. 아래 그림은 불연속 분포를 가지는 pmf를 정리한 것이다.

정리되어 있는 확률분포 중에 관심이 생기는 분포가 있다면 위키피디아에서 자세히 알아보는 것을 추천한다.
끝으로
이번 글에서는 확률변수에 이어서 확률밀도함수(pdf)에 대해서 알아보았습니다. pdf는 확률변수를 이용하기 위한 하나의 도구입니다. 이해하고 유익한 pdf에 대해서는 한번 유도해보는 것도 좋은 경험이 될 것 같습니다.
'확률' 카테고리의 다른 글
| 공학 확률 - (1) 확률과 확률변수(Random variable) (0) | 2020.05.30 |
|---|