ROC 곡선 (ROC curve) - (1) 기본개념

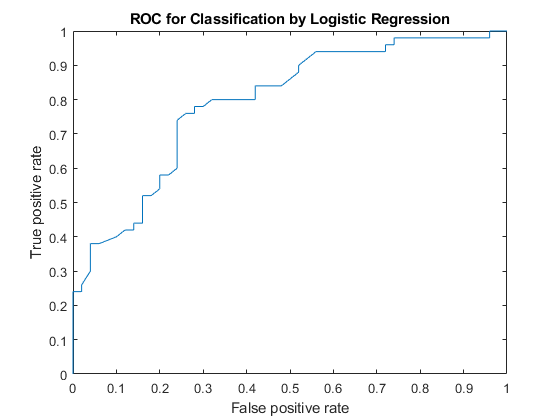
 이번 글에서는 진단 역량을 평가하기 위한 이진분류법을 기반으로 만들어지는 ROC 곡선(Receiver operating characteristic curve)에 대해서 알아보고자 한다.  ROC 곡선은 아래와 같이 FPF(False Positive Rate)와 TPF(True Positive Rate)로 그려지는 그래프를 말한다. ROC곡선은 의학 분야에서 진단의 목적으로도 많이 사용될 뿐만 아니라 머신러닝(Machine Learning)에서 개발된 알고리즘의 성능 평가의 목적으로도 흔히 사용되는 지표이므로 이에 대해 높은 이해도를 가진다면 연구에 큰 도움이 될 것이다.

 

<ROC 곡선>

---

1. ROC 곡선의 필요성

 우리는 평가를 할때 항상 정량적인 수치로 유동적인 처방을 내릴 수 있으면 좋겠지만 대개는 양성/음성, 참/거짓, 혹은 유죄/무죄와 같이 이진분류를 해야하는 순간이 많다. ROC 곡선은 이진분류에서 가장 흔히 사용되는 평가 방법이다. ROC 곡선을 이용하면 이진분류에 사용되는 결정 기준(Discrimination threshold) 혹은 결정 변수(Decision variable)의 변화에 따라 진단 역량의 변화를 시각적으로 표현할 수 있다. 그리고 이를 통해서 최종적인 결정 기준을 선정하기도 한다.

 

 말이 좀 어려워졌는데 ROC 곡선의 목적을 쉽게 한마디로 정리하자면 "이진분류 상황에서 특정 결정 기준에 대한 진단 능력 시각화" 라 이해하면 될 것 같다.

 

 그렇다면 진단 능력 시각화가 왜 필요할까?

 

 진단에는 많은 결정 기준이 있을 수 있다. 이미 있는 것도 있을 것이고 새로운 진단법이 개발되어 추가된 결정 기준도 있다. 각 결정 기준의 진단 능력을 시각화하면 효과적으로 서로를 비교할 수 있다. 그래서 그 중에서 가장 좋은 진단법을 가려낼 수도 있고 더 나아가 최적의 기준을 도출할 수도 있다. 거의 모든 이진분류 상황에서 결정 기준을 평가할 때 ROC 곡선을 사용하고 있다.

---

2. ROC 곡선의 이해

 하나의 예를 들어보자. 코로나19 의심환자에 대해서 검진을 실시했다고 하자. 환자는 음성집단(병이 없는 집단)과 양성집단(병이 있는 집단)이 있을 것이다 (아래 그림에서 빨간색 분포(\( P(n) \))와 초록색 분포(\( P(s) \))). 그리고 바이러스 검사는 환자의 시료를 토대로 측전된 수치가 기준치 이상이라면 양성, 그 반대로 이하라면 음성이라 판단한다. 이때 여기서 말하는 시료의 수치가 결정 기준 혹은 결정 변수이 된다. 아래 그림에서는 결정변수가 \( x \)이고 기준치는 아래 그림에서 \( x' \)이다.

 

<결정변수 x에 대한 음성집단과 양성집단의 분포>

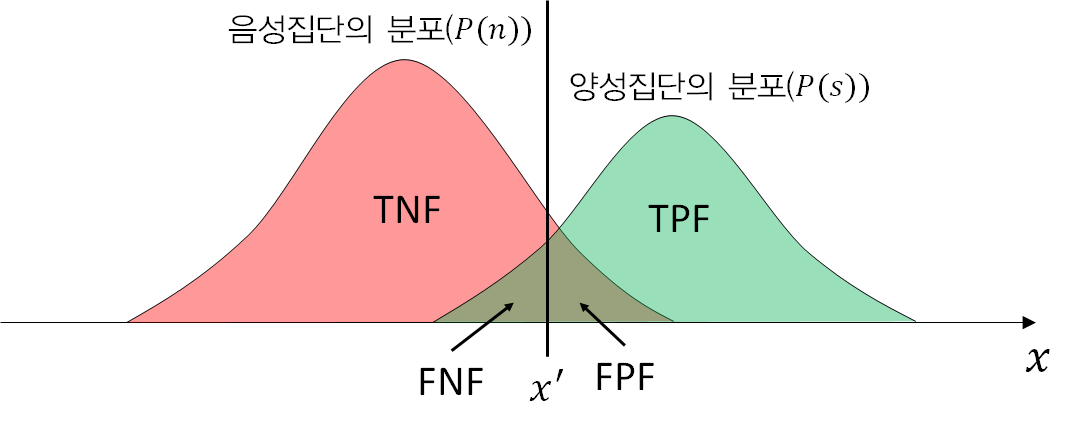
 그렇다면 검진에서 나올 수 있는 경우의 수는 총 4가지이다. 음성환자인데 음성이 나올 경우, 음성환자인데 양성이 나올 경우, 양성환자인데 음성이 나올 경우 혹은 양성환자인데 양성이 나올 경우.

 

위 4가지를 확률로 계산한 것을 TNF(True Negative Fraction), FPF(False Positive Fraction), FNF(False Negative Fraction), TPF(True Positive Fraction)라고 한다.

 

TNF = 음성집단에서 테스트 결과 음성이라 나올 확률 \( = P(Test-|n)\)
FPF = 음성집단에서 테스트 결과 양성이라 나올 확률 \( = P(Test+|n)\)
FNF = 양성집단에서 테스트 결과 음성이라 나올 확률 \( = P(Test-|s)\)
TPF = 양성집단에서 테스트 결과 양성이라 나올 확률 \( = P(Test+|s)\)

여기서 TNF는 민감도(Sensitivity), TNF는 특이도(Specificity)라 불리기도 한다.

---

ROC 곡선은 어떻게 그리나요?

 

 다시 위의 음성집단과 양성집단 분포 그래프를 보자. TNF, FPF, FNF, TPF의 값은 크게 기준치 \( x' \)에 영향을 받는다. 기준치가 어디에 위치하냐에 따라서 TPF와 FPF 확률이 0으로 가기도하고 1로 갈 수도 있다. 이것을 이해했다면 ROC 곡선을 절반이상은 이해한 것이다.

 

 ROC 곡선이 바로 기준치 \( x' \)를 \( -\infty \)에서 \( \infty \)까지 움직이면서 계산된 TPF를 y축, FPF를 x축에 그린 것이다.  아래 그림을 참고하자.

 

<기준치에 따른 ROC 곡선 내의 좌표 위치>

 

 ⓐ부터 시작해서 ⓑ, ⓒ, ⓓ로 \( x' \)이 움직이면서 오른쪽의 ROC곡선이 그려진다. 그림은 불연속적이지만 연속적으로 생각하면 금방 이해할 수 있을 것이다.

 

---

끝으로

 이번 글에서는 ROC곡선에 대한 기본적인 정의와 ROC곡선을 그리는 방법에 대해서 알아보았습니다. 글이 너무 길어지므로 잠깐 끊고 다음 글에서는 조금더 응용하여 ROC곡선을 이용한 결정인자 비교법 및 AUC에 대해서 알아보도록 하겠습니다.

 

 

 

 

※ 본 글이 도움되었다면 하트 클릭 부탁드립니다!

(비로그인으로도 가능합니다! )